Cryptographic Hash Functions & Digital Signatures

Understanding Bitcoin on a deep technical level

Disclaimer: Content is summarised from Chapter 2 of 'Grokking Bitcoin' by Kalle Rosenbaum

Contents:

2. Cryptographic Hash Functions & Digital Signatures • The cookie token spreadsheet • Cryptographic hashes

• Digital Signatures

• Summary

2.1 The cookie token spreadsheet

E.g. There’s a cafe in the office where you work. Your office uses a spreadsheet to keep track of cookie tokens, CT. You can exchange CT for cookies in the cafe.

Lisa stores this spreadsheet on her computer. It’s shared read-only for everybody on the office network to open and watch, except Lisa. Everybody trusts her. She has full access to do whatever she likes with the spreadsheet.

If Alice wants a cookie, she asks Lisa, who sits right next to the cafe, to transfer 10 CT from Alice to the cafe. Lisa knows who Alice is & can verify in the spreadsheet that she owns enough cookie tokens; she’ll search for “Alice” & sum all amounts with Alice’s name in the To column & subtract all amounts with Alice’s name in the From column. Lisa calculates that Alice has 70 CT, enough for Alice to pay 10 CT to the cafe. She appends a row at the end of the spreadsheet.The cafe sees this new row in the spreadsheet & hands a cookie over to Alice.

Table 2.2 is your starting point for learning how BTC works. Every chapter will take us closer to the end result: Bitcoin.

2.2 Cryptographic Hashes

A person produces the same fingerprint of her left thumb every time it’s taken,

but it’s extremely hard to find another person with the same fingerprint. The fingerprint doesn’t disclose any info about the person. Cryptographic hashes are used everywhere in BTC. Think of a cryptographic hash as a fingerprint. To create a cryptographic hash of a file, you send the file into a computer program; "cryptographic hash function".

A bit is the smallest unit of info in a computer. It can take either of 2 values: 0 or 1. A byte is 8 bits that together can take 256 different values. We often use hexadecimal, or hex, encoding when we display numbers in this book. Each byte is printed as 2 hex digits each in the range 0–f, where a = 10 and f = 15.

E.g. Creating a cryptographic hash of a cat picture

Output; "hash", is a 256-bit number; 256 bits = 32 bytes as 1 byte consists of 8 bits. Compare that to the size of the cat picture is 1.21 MB. The particular cryptographic hash function used in this e.g. is"SHA256" (Secure Hash Algorithm with 256-bit output) & is the most commonly used one in BTC.

"Hash" means something that’s chopped into small pieces or mixed up. Cryptographic hash function takes the cat picture & performs a mathematical calculation on it. Out comes a big number, cryptographic hash, that doesn’t look remotely like a cat. You can’t “reconstruct” the cat picture from just the hash; a cryptographic hash function is a one-way function. When you change the cat picture a little & run it through the same cryptographic hash function, hash turns out completely different but the length of the hash is always the same regardless of input.

Why are cryptographic hash functions useful?

Cryptographic hash functions can be used as an integrity check to detect changes in data. E.g. you want to store a cat picture on your laptop’s hard drive, but you suspect the stored picture might become corrupted. This could happen e.g. due to disk errors or hackers. To detect corruption: First, calculate a cryptographic hash of the cat picture on your hard drive & write it down on a piece of paper. Later, calculate the cryptographic hash of the cat picture again & compare it to the original hash. (There’s a tiny chance the cat picture has changed even if the hashes match. But that chance is so small, you can ignore it)

BTC uses cryptographic hash functions to verify that data hasn’t changed. E.g. ~ every 10 min, a new hash of the entire payment history is created. If someone tries to change the data, anyone verifying the hash of the modified data will notice.

How does a cryptographic hash function work?

We’ll create a very simplistic one. We'll call it a hash function for now. E.g. you want to hash a file containing 6 bytes: a1 02 12 6b c6 7d. You want the hash to be a 1-byte number (8 bits). You can construct a hash function using "addition modulo 256", which means to wrap around to 0 when the result of an addition reaches 256

Modulo means to wrap around when a calculation reaches a certain value.

E.g.

• 0 mod 256 = 0

• 255 mod 256 = 255

• 256 mod 256 = 0

• 257 mod 256 = 1

• 258 mod 256 = 2

Result is the decimal number 99. If you change the input, hash will change, but there is a chance the hash remains 99 as this simple hash function has just 256 different possible outputs. With real cryptographic hash functions, like the one we used to hash the cat picture, this chance is unimaginably small.

Properties of a cryptographic hash function

A cryptographic hash function takes any digital input data, "pre-image" & produces a fixed-length output, "hash". E.g. pre-image is the cat picture of 1.21 MB & hash is a 256-bit number. Hash is aka "digest".

Basic properties you can expect from a cryptographic hash function (using SHA256)

1. Same input will always produce the same hash

2. Slightly different inputs will produce very different hashes

3. Hash is always of the same fixed size. For SHA256, it’s 256 bits.

4. Brute-force trial & error is the only known way to find an input that gives a certain hash

There are some variations to 4th property, all of which are desirable for cryptographic hash functions

• Collision resistance: only have the cryptographic hash function. It’s hard to find 2 different inputs that result in the same hash

• Pre-­image resistance: only have the hash function & a hash. It’s hard to find a pre-­image of that hash

• Second ­pre­-image resistance: only have the hash function & a pre-image (& thus hash of that pre-image). It’s hard to find another pre-image with the same hash

Illustration of “hard”

E.g. second-pre-image resistance: find an input to SHA256 that results in the same hash as “Hello!”: 334d016f755cd6dc58c53a86e183882f8ec14f52fb05345887c8a5edd42c87b7334d016f755cd6dc58c53a86e183882f8ec14f52fb05345887c8a5edd42c87b7

Only way to find an input besides “Hello!” that gives the same hash is to try different inputs one by one & check if the desired hash is produced

A desktop computer can calculate ~ 60 million hashes per second & expected number of tries needed is 2^255. 2^225 / (60 × 10^6) s ≈ 10^68 s ≈ 3 × 10^61 years Pre-image resistance, second-pre-image resistance & collision resistance are extremely important in BTC. Most of its security relies on these properties

Some well-known hash functions

We most often use double SHA256 in BTC:

Generally, when a single collision has been found in a cryptographic hash function, most cryptographers consider the function insecure.

2.3 Digital Signatures

You can prove to others that you approve a payment with a digital signature. Digital signatures are tied to a private key & are much harder to forge than a handwritten signature.

Typical use of digital signatures

E.g. you want to send a cat picture to your friend Fred via email, how would you & Fred ensure the picture Fred receives is exactly the same?

Include a digital signature of the cat picture in the email. Fred can verify this digital signature to ensure the cat picture is authentic:

Step 1 (preparation): create the private key to create digital signatures. Then create the public key to verify the signatures the private key creates. Public key is calculated from the private key. Hand the public key over to Fred in person so Fred is sure it belongs to you.

Step 2 (signing): write an email to Fred & attach the cat picture. Also use your private key & the cat picture to digitally sign the cat picture. Result is a digital signature that is included in the email message. Send the email to Fred.

Step 3 (verifying): Fred uses the public key he got from you in step 1, the digital signature in the email & attached cat picture. If the signature or the cat picture has changed since you created the signature, the verification will fail.

Improving cookie token security

Lisa has a hard time recognising everyone & notices that some aren’t honest. E.g. Mallory says she is Anne, to trick Lisa into moving CT from Anne to the cafe. Lisa thinks of requiring everybody to digitally sign their CT transfers by writing a message & a digital signature in an email.

John wants to buy a cookie in the cafe for 10 CT. He needs to digitally sign a CT transfer

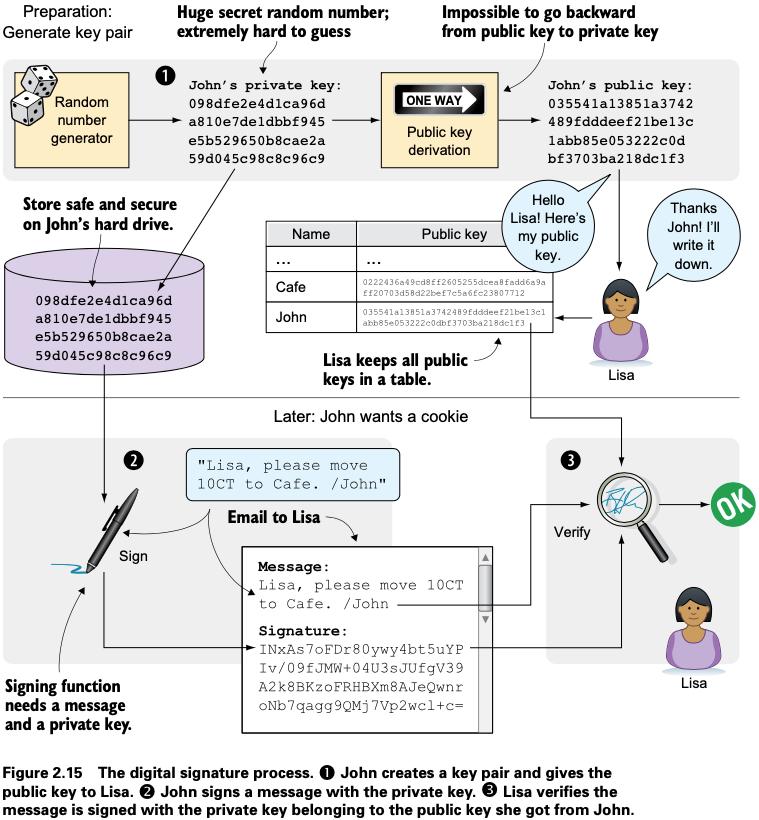
3 phases in this process:

1. John prepares by generating a key pair. John keeps the private key secret & hands the public key over to Lisa. This is a one-time setup step.

2. John wants a cookie. He writes a message & signs it with his private key. He sends the message & digital signature in an email to Lisa.

3. Lisa verifies the signature of the message using John’s public key & updates the spreadsheet.

1. Preparation: John generates a key pair

Key pair is created once. Same private key can be used several times for digitally signing. Signing & verification processes are based on a key pair. John needs a private key to sign payments & Lisa will need John’s public key to verify John’s signatures. John needs to prepare for this by creating a key pair by first generating a private key & then calculating the public key from that private key

John uses a random number generator to generate a huge, 256-bit number which is now John’s private key. Private key is transformed into a public key using a public-key derivation function which is a one-way function, just like cryptographic hash functions; you can’t derive the private key from the public key. Security of digital signatures relies heavily on this feature. Running the private key through the public-key derivation function multiple times will always result in the same public key.

Public key is 33 bytes (66 hex digits) long. Private key is 32 bytes (64 hex digits) long.

2 Ways to Use the Key Pair

Keys are used to encrypt & decrypt data. Encryption makes messages unreadable unless you hold the proper decryption key. Public key can be used to encrypt messages that only the private key can decrypt & private key can encrypt messages that can only the public key can decrypt.

Left side of figure 2.17: Only John would be able to read the encrypted message as he’s the only one with access to his private key. BTC doesn’t use this feature of public & private keys at all. It’s used when 2 parties want to communicate in private e.g. online banking. When you see the little padlock in the address bar of your web browser, then you know the process shown on the left side of the figure is being used to secure your communication.

Right side: Lisa can decrypt the message as she has the public key belonging to John’s private key. This feature is used for digital signatures. Using the private key to encrypt secret messages isn’t a good idea as the public key is public. But digital signatures don’t need any secret messages.

2. Signing: John signs his payment

Message John wants to sign is, “Lisa, please move 10CT to Cafe. /John”. Signing function will hash this message with SHA256 & hash value is then encrypted with John’s private key. Result is a digital signature that looks like this: INxAs7oFDr80ywy4bt5uYPIv/09fJMW+04U3sJUfgV39A2k8BKzoFRHBXm8AJeQwnroNb7qagg9QMj7Vp2wcl+c=

Signature is an encrypted hash of a message. If John used another private key to sign with or a slightly different message, signature would be completely different. John sends the email containing a message & a signature of that message to Lisa.

3. Verifying: Lisa Verifies the Signature

Lisa aims to determine that the CT transfer was signed by the private key it claims to be signed with. She had already received John’s public key. The things she has at hand are:

(a) Message “Lisa, please move 10CT to Cafe. /John”

(b) Signature "INxAs7oFDr8..."

(c) John’s public key that she just looked up in her table

John encrypted the message’s hash with his private key. This encrypted hash is the signature. If Lisa decrypts the signature with John’s public key , result should be a hash that equals the hash of the message in the email.

Lisa hashes that message just like John did when he created the signature. The message hash & decrypted signature match, thus signature is valid.

Note: this process only works if John & Lisa use the same digital signature scheme. This must be agreed on beforehand. In BTC, everyone knows what digital signature scheme to use.

Lisa updates the spreadsheet with John’s transfer.

Private Key Security

John is in control of his CT as he owns the private key. If his private key is stolen, he can lose his CT. John’s writes an email to Lisa: "Good morning Lisa! Please move 20 CT to Cafe. /John Signature: H1CdE34cRuJDsHo5VnpvKqllC5JrMJ1jWcUjL2VjPbsjX6pi/up07q/gWxStb1biGU2fjcKpT4DIxlNd2da9x0o="

He sends this email containing the message & a signature to Lisa. But the cafe doesn’t hand him any cookies. John opens the spreadsheet & searches for “John.”

Lisa says that she got a message signed with John’s private key, asking her to send money to a new coworker, Melissa. But there is no Melissa at the office. Lisa needs the name to look up the correct public key in the table.

Explanation is that Mallory has:

1. Managed to copy John’s private key. John’s laptop was on his desk all night long. Anyone could have taken the hard drive out of the laptop to search for his private key.

2. Created a new key pair & sent the new public key to Lisa, with the following message:

Hi Lisa. My name is Melissa, and I’m new here.

My public key is 02c5d2dd24ad71f89bfd99b9c2132f796fa746596a06f5 a33c53c9d762e37d9008

3. Sent a fraudulent message, signed with the stolen private key, to Lisa as follows:

Hi Lisa, please move 90 CT to Melissa. Thanks, John Signature: IPSq8z0IyCVZNZNMIgrOz5CNRRtRO+A8Tc3j9og4pWbAH/zT22dQEhSaFSwOXNp0lOyE34d1+4e30R86qzEbJIw=

Lisa verified the transfer in step 3, concluded it was valid & executed the transfer. John asks Lisa to revert the transfer. But Lisa refuses as she thinks the transfer is perfectly valid. If John let someone see his private key, that’s his problem, not Lisa’s.

John creates a new key pair & asks Lisa to add his new public key under the name John2. How can John secure his new private key & still have it readily available when he wants a cookie? John is pretty sure he won’t have more than 1,000 CT on that key.

Security of the spreadsheet has shifted from a system in which Lisa knows everyone’s face to one in which she knows everyone’s public key. Security could be worse now as it might be easier for Mallory to steal John’s private key than it is for her to trick Lisa into thinking Mallory is John. This depends on how John protects his private key. No one will be able to restore John’s private key if he loses it & Lisa sure isn’t going to reverse “fraudulent” transfers if John is sloppy with security.

If John stores private key in an encrypted file, protected by a strong password, on his own laptop’s hard drive, getting a copy of his key is a lot harder. An attacker would have to

1. Access John’s hard drive 2. Know John’s password

John's concern for security depends on how many CT he has on his private key.

Trade-off exists between security & convenience. Some of the different trade-offs:

1. Online vs. offline: Online means private key is stored on a device with network access, like mobile phone or laptop. Offline means private key is stored on a piece of paper or a computer without any network access. Online storage is risky as remote security exploits or malicious software on your computer might send the private key to someone without you noticing. If the device is offline, no one can take the private key without physical access to the device.

2. Cleartext vs. encrypted: If private key is stored in cleartext in a file on your computer’s hard drive, anyone with remote or physical access to your computer can copy the private key. Avoid many of these attacks by encrypting your private key with a password that only you know. An attacker would then need access to both your hard drive and your secret password to get the private key.

3. Whole key vs. split key: People usually store their entire private key on a single computer. This is convenient. But if your private key is split into e.g. 3 parts & you store them separately on 3 computers, then the attacker must access all 3 hard drives making it much harder as they must know which 3 computers to attack & successfully attack them. Making a payment in this setup is a real hassle, but very secure.

As a rule of thumb, greater the security against attackers, the greater the risk of you accidentally losing access to your key. E.g. if you store the private key encrypted on your hard drive, you risk losing your key due to both computer failure & forgetting your password.

2.4 Summary

• Bitcoins are created as rewards to nodes securing the blockchain

• Reward halves every 4 years to limit the money supply

• Cryptographic hash functions can detect changes in a file or a message

• You can’t make up a pre-image of a cryptographic hash. A pre-image is an input that has a known output

• Digital signatures prove a payment’s authenticity. Only the rightful owner of bitcoins may spend them

• To verify a digital signature one just needs to know that the signature was made with the private key the signature claims to be signed with (don't need to know who made it)

• To receive bitcoins, you need a public key. First, create a private key then derive the public key

• Several strategies are available for storing private keys e.g. unencrypted on your mobile phone, split or encrypted across several offline devices

• The more secure the private key is against theft, the easier it is to accidentally lose the key